Einführung in dem Dampfkraftwerk

„ In Sinn der Umwandlung von Wärme in technischen Arbeit

mit Helfe einen Dampfkraftprozess “

Mohamed Shaalan

Inhalt

1. Allgemeine thermodynamische Grundlagen

1.1. Carnot-Prozess

1.2. Zustandsvariablen des Arbeitsmittels durch die Anwendung den Hauptsätze der Thermodynamik

1.2.1. die innere Energie (u)

1.2.2. die spezifische Enthalpie (h)

1.3. Nutzarbeit und Wirkungsgrad von Carnot-Prozess

1.3.1. Nutzarbeit

1.3.2. Wirkungsgrad

1.4. die Wärmemenge und die Exergie

2. Thermodynamische Grundlagen den Dampfkraftwerken

2.1. der ideale (einfache) Clausius-Rankine-Prozess

2.1.1. Kreisverlaufbeschreibung

2.1.2. Zustandesdiagramme zur Darstellung von Clausius-Rankine-Prozess

2.1.2.1.T,s-Diagramm

2.1.2.2.h,s-Diagramm

2.2. der thermische Wirkungsgrad von Dampfkraftwerken

3. Maßnahmen zur Verbesserung des thermischen Wirkungsgrades beim Clausius-Rankine-Prozess

3.1. Zwischenüberhitzung

3.2. regenerative Speisewasservorwärmung

4. Beispiele für Stationen mit Dampfkraftprozess

4.1. Grundfließbild der Harry Allen Station

5. Fragen

6. Literatur

1- Allgemeine thermodynamische Grundlagen

Die Anwendung von Wärme in Arbeit wird mit Helfe von Dampf Kreisprozessen durchgeführt.

Dabei wird einem Arbeitsmittel (Dampf) Hochtemperaturwärme zugeführt. Das Arbeitsmittel leistet in der Maschine mechanische Arbeit, die als Nutzarbeit entnommen werden kann.

Ein Kreisprozess ist dadurch gekennzeichnet, dass der Endzustand der Arbeitsmittel nach einer Reihe von Zustandsänderungen wieder mit dem Anfangzustand identisch ist.

1.1. Carnot-Kreisprozess

Unter den Kreisprozessen spielt der von Carnot eingeführte Prozeß eine besondere Rolle.

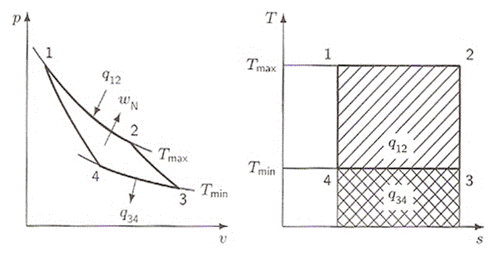
Abb.: Carnot-Prozess in p,v- und T,s-Diagramm [3]

· Bei Carnot-Prozess läuft das Arbeitsmittel in folgenden Zustandsänderungen:

a) 1-2: Isotherme Expansion unter Zufuhr der Wärme ( q₁₂ = q _zu ),

b) 2-3: Isentrope Expansion unter Abgabe der Arbeit (w₂₃),

c) 3-4: Isotherme Kompression unter Abfuhr der Wärme (q₃₄ = q_ab),

d) 4-1: Isentrope Kompression unter Zufuhr der Arbeit (w₄₁).

Bei jedem Prozess wird vorausgesetzt, dass der Zustand des Arbeitsmittels durch ein Variablenpaar (z.B. p-v, T-s oder h-s) eindeutig festgelegt ist.

Bei der Kraftmaschine (Arbeitmaschine), die die thermische Energie in mechanische Energie (Arbeit) umwandelt „Turbine“, wird aus dem Prozess die Arbeit „w“ entnommen werden.

· Der Betrag diese Arbeit erscheint als Fläche in p,v-Diagramm, es ergibt:

§ w….. geleistete technische Arbeit in (kJ/kg),

§ v…... spezifisches Volumen des Arbeitsmittels in (m³/kg)

§ p ….. Druck in (MPa)

· Entsprechend sind die zu dem Prozess zugeführte und die von ihm abgegebene Wärme (q_{zu ,} q_ab) als Fläche im T,s-Diagramm.

Aus dem Definition der Entropie (dq = T ds) folgt für die Summe der zu- und abgeführten Wärmemengen:

§ q …….....zu- und abgeführte Wärme in (kJ/kg)

§ T………..Temperatur in (K)

§ s………..spezifesche Entropie des Arbeitsmittels in (kJ/kg.K)

Für die Anwendung des 1.Hauptsatzes der Thermodynamik auf den Kreisprozess erfolgt, dass alle zu dem Prozess zugeführte Energie positiv und die aus dem Prozess abgegebene Energien negativ sind.

Dabei kann das letzte Kreisintegral in zu- und abgeführte Wärme zerlegt werden, es folgt:

§ q………….zu- und abgeführte Wärme in (kJ/kg)

§ q_zu…….…..zugeführte Wärme in (kJ/kg)

§ q_ab ………..abgeführte Wärme in (kJ/kg)

§ T_max ….…..oberes Temperaturniveau in (^oC)

§ T_min ……...unteres Temperaturniveau in (^oC)

§ s……….…spezifesche Entropie des Arbeitsmittels in (kJ/ kg.K)

1.2. Zustandsvariablen des Arbeitsmittels durch die Anwendung

den Hauptsätzen der Thermodynamik:

1.2.1. die spezifische innere Energie (u)

der 1.Hauptsatz sagt, dass die zu einem System zugeführte Energie der Änderung seiner gespeicherten Energie, d.h. seiner inneren Energie, entspricht.

Da bei einem Kreisprozess die Anfangs- und Endzustand identisch sind, d.h. ändert sich die innere Energie nicht, daraus folgt:

§ u………….spezifesche innere Energie in (kJ/kg)

§ q………….zu- und Abgeführte Wärme in (kJ/kg)

§ w…………geleistete technische Arbeit in (kJ/kg)

§ v…………..spezifisches Volumen des Arbeitsmittels in (m³/kg)

§ p……….…Druck in (MPa)

die innere Energie ist eine den Zustandsvariabeln des Arbeitsmittels, sie hängt davon ab:

- momentanem Druck und,

- momentanem spezifischem Volumen.

u = u (T,v)

die innere Energie nimmt bei konstanten Volumen ungefähr proportional zur Temperatur des Arbeitsmittels zu, es gibt:

du = c_v .dT

die spezifische Wärme bei konstanten Volumen (c_v) ist eine Proportionalsfaktor und für ideale Gase Konstant.

1.2.2. die spezifische Enthalpie (h)

Neben der spezifischen inneren Energie wird noch die spezifische Enthalpie als eine den Zustandsvariablen des Arbeitsmittels verwendet.

Sie ergibt sich aus der Zusammensitzung der inneren Energie und der Volumenarbeit (pv), wie folge:

§ h ………spezifische Enthalpie des Arbeitsmittels in (kJ/kg)

§ u ……….spezifische inneren Energie des Arbeitsmittels

§ v ………..spezifische Volumen des Arbeitsmittels in m³/kg

§ P ………Druck in MPa

Die Enthalpie nimmt bei konstantem Druck proportional zur Temperatur des Arbeitsmittels zu,

h = h ( T , p )

es gibt:

dh = c_p.dT

die spezifische Wärme beim konstanten Druck (c_p) ist für ideale Gase konstant.

1.3. Nutzarbeit und Wirkungsgrad von Carnot-Prozess

1.3.1. die Nutzarbeit ()

sie ist gleich der Differenz zwischen den zu- und abgeführten Wärmen, es gibt:

§ …………….Nutzarbeit in (kJ/kg)

§ ………….. zugeführte Wärme in (kJ/kg)

§ …………….Abgeführte Wärme in (kJ/kg)

1.3.2. der thermische Wirkungsgrad

Er ist das Verhältnis aus der Nutzarbeit, die von einem Prozess entnehmbar ist, und der Energie, die zur Durchführung des Prozesses aufgewendet ist.

Der thermische Wirkungsgrad ist als die Umwandlung der Hochtemperaturwärme in Nutzarbeit definiert, es gibt:

§ ………....thermische Wirkungsgrad des Carnot-Prozesses

§ ………...zugeführte Wärme in (kJ/kg)

§ ………....abgeführte Wärme in (kJ/kg)

§ ………..oberes Temperaturniveau in (^oC)

§ ………..unteres Temperaturniveau in (^oC)

· Der Carnot-Prozess zeigt, dass zur Gewinnung von technischen Arbeit aus Wärme mit einem Kreisprozess muss zu dem Prozess Wärme auf einem hohen Temperaturniveau zugeführt und dann auf einem tieferen Temperaturniveau entzogen werden.

Bei einem reversiblen Carnot-Prozess ist wegen ( ), und aus der Entropie Definition ( dq = T ds ) , folgt:

§ s……………spezifesche Entropie des Arbeitsmittels in (kJ/kg.K)

§ q…………...zu- und abgeführte Wärme in (kJ/kg)

§ q_zu……...…..zugeführte Wärme in (kJ/kg)

§ q_ab ………….abgeführte Wärme in (kJ/kg)

§ T_max …….....oberes Temperaturniveau in (^oC)

§ T_min ………..unteres Temperaturniveau in (^oC)

In der Realität kann die Wärme bei einem Prozess nicht vollständig in Arbeit umgewandelt werden, d.h. kann nicht reversibel Laufen. Da spricht man von irreversiblem Prozess.

· Ein Prozess verläuft irreversibel wenn:

1- bei irgendeinem Teil des Prozesses Arbeit in Wärme umgewandelt wird,

2- bei einem Teilvorgang Wärme ohne Arbeitsleistung von einem höheren auf einem tieferen Temperaturniveau fließt.

Solche Effekte können bei wirklichem Kreisprozessen nicht vermeiden werden, deshalb ist:

§ …………thermische Wirkungskrad eine einfache Dampfkraftprozess

§ …………thermische Wirkungsgrad des idealen Carnot-Prozesses

1.4. die Wärmemenge () und die Exergie () eines Prozesses

eine Wärmemenge () von einem höheren Temperatur als die Umgebungstemperatur (T_u) kann höchstens zu einem Teil () in nutzbare Arbeit umgewandelt werden.

Diesen umwandelbaren Anteil bezeichnet man als Exergie.

Der nicht in Arbeit umwandelbare Teil von der Wärmemenge bezeichnet man als Anergie (), daraus ergibt sich:

= +

Es bleibt anzumerken, dass die Exergie verloren gehen kann. Man spricht dann von einem Exergieverlost oder weniger genau von einem Energieverlost.

2. thermodynamische Grundlagen den Dampfkraftwerken

2.1. der ideale Clausius-Rankine-Prozeß „CRP“

der bei den Dampfkraftwerken eingesetzte Kreisprozess ist der Clausius-Rankine-Prozeß.

Als Arbeitsmittel wird Wasser verwendet.

Ein einfacher Clausius-Rankine-Prozeß ist aus den Komponenten folgenden Komponenten aufgebaut:

- Dampferzeuger,

- Dampfturbine,

- Kondensator und

- Speisewasserpumpe.

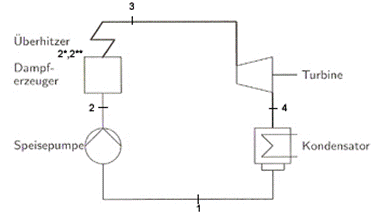
Abb.: notwendige Komponenten einer Dampfkraftanlage [3]

die Phasenumwandlung (flüssig/ gasförmig) wird im Dampferzeuger und die Wandlung (gasförmig/ flüssig) wird im Kondensator stattfinden.

2.1.1. Kreisverlaufbeschreibung

(1à2): es ist die erst Schritt dabei wird den Druck des Speisewassers in der

Speisewasserpumpe auf einem Druck zwischen 30-300 bar gebracht,

(2à3): die Wärmezufuhr „“ erfolgt in einem Dampferzeuger, in dem das

Wasser zu nächst auf die Siedetemperatur, die dem Betriebsdruck entsprecht, erwärmt wird (2 à 2^*) , verdampft (2^* à 2^**) und schließend auf Temperatur zwischen 400-600 ^oC überhitzt wird (2^** à 3),

(3à4): der so erzeugte Frischdampf wird anschließend in einer Dampfturbine auf dem

in Kondensator herrschenden Druck entspannt. Die dabei geleistete Arbeit wird im Generator in elektrische Energie umgewandelt,

(4à1): die Wärmeabfuhr erfolget im Kondensator nahezu bei Umgebungstemperatur.

2.1.2. Zustandesdiagramme zur Darstellung von Clausius-Rankine-

Prozess

Die ablaufenden Arbeitsmittelzustandesänderungen im Clausius-Rankine-Prozess werden in folgenden Diagrammen dargestellt:

2.1.2.1 T,s-Diagramm

Das T,s-Diagramm ist ein wichtiges Hilfsmittel von der Berechnung von Kreisprozessen, da sich reversibel ausgetauschte Wärmemengen gemäß der folgenden Beziehung als Fläche dargestellten lassen.

§ q …………… die ausgetauschte Wärmemenge in (kJ/kg)

§ T……………die Temperatur des Arbeitsmittels in (K)

§ s …………….spezifische Entropie des Arbeitsmittels in (kJ/kg.K)

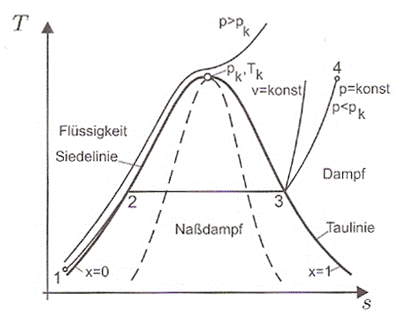
Abb.: Clausius-Rankine-Prozess im T,s-Diagramm für

Wasser (p_k=221,20 bar, T_k=374,15 ^oC) [3]

Man bezeichnet die Zustände auf der Siedelinie mit und auf der Taulinie mit .

· Verlauf des Arbeitsmittels in dem Dampferzeuger:

Im Diagramm ist einen isobaren Zustand (1 à 4) eingezeichnet.

(1à2) Um die Flüssigkeit von Flüssigkeitszustand (1) ausgehend zum Sieden zu

bringen, ist pro Masseneinheit die folgende Wärme zuzuführen:

§ …………zugeführte Wärme in (kJ/kg)

§ ………….spez. Wärmekapazität des Arbeitsmittels in (kJ/ kg.K)

§ …………...Temperatur des Arbeitsmittels in (K)

(2à3) Im Zustand (2) beginnt die Flüssigkeit zu sieden.

Bei gleichbleibender Temperatur geht mehr und mehr Flüssigkeit in die Dampfphase über. Dazu ist die folgende Verdampfungsenthalpie erforderlich:

§ ……....Verdampfungsenthalpie des Arbeitsmittels (Wasser) in

(kJ/kg)

§ ………....Temperatur des Arbeitsmittels in (K)

§ ……….…Entropie der siedende Flüssigkeit in (kJ/ kg.K)

§ ……...…Entropie des gesättigtes Dampf in (kJ/kg.K)

§ ..…….... Enthalpie der siedende Flüssigkeit in (kJ/kg)

§ ….……. Enthalpie des gesättigtes Dampf in (kJ/kg)

Zum Beschreibung eines Zustandes in Naßdampfgebet (Flüssigkeit/Dampf) es ist außer Druck und Temperatur noch eine weitere Größe notwendig.

Es ist üblich, hier dafür den Dampfgehalt (x) als Zustandesgröße zu verwenden.

Bei (x = 0) siedet die Flüssigkeit, und bei (x = 1) liegt trocken gesättigter Dampf vor.

(3 à 4) zur Überhitzung des trocken gesättigter Dampfes ist noch folgende

Wärme notwendig:

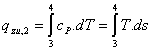
§ ………zugeführte Wärme in (kJ/kg)

§ ……….spez. Wärmekapazität des Arbeitsmittels in (kJ/ kg.K)

§ s ………….spezifische Entropie des Arbeitsmittels in (kJ/kg.K)

§ ………..Temperatur des Arbeitsmittels in (K)

· Im gesamten Prozessverlauf werden folgende Zustandesänderungen des Arbeitsmittels vorgenommen:

a. (1 à 2): Isentrope Verdichtung in der flüssigen Phase,

b. (2 à 3): Isobare Wärmezufuhr ( Vorwärmung, Verdampfung und

Überhitzung),

c. (3 à 4): Isentrope Expansion,

d. (4 à 1): Isobare Wärmeabfuhr und Kondensation.

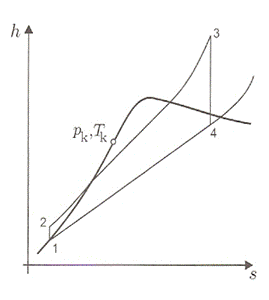
2.1.2.2. h,s-Diagramm

Zur Darstellung des Prozeßverlaufes in der Turbine wird meinst das h,s-Diagramm verwendet.

Im h,s-Diagramm können besonders folgende als Strecken abgegriffen werden:

- die isobare ausgetauschte Wärmemengen und

- die bei isentroper Zustandesänderung ausgetauschte mechanische Arbeit.

.....Nutzarbeit der

Turbine

....Wärmeabgabe im

Kondensator

…Energiezufuhr der

. Speisepumpe

...Wärmezufuhr im

Dampferzeuger

Abb.: Clausius-Rankine-Prozess im h,s-Diagramm [3]

2.2. der thermische Wirkungsgrad von Dampfkraftwerken

eine thermische Wirkungsgrad für die Umwandlung von Wärme in mechanische Arbeit in Dampfkraftwerk mit Clausius-Rankine-Prozess wird berechnet in dem schnittweise die Wärmeströme, den einzelnen Komponenten zu- und abgeführt sind, und die zu- und abgeführte Arbeit bilanzieren werden.

man kann es mit der Bezeichnungen aus dem (h,s-Diagramm) in Allgemeine wie folge definieren:

§ …………..thermische Wirkungsgrad des Prozesses

§ …………….Nutzarbeit aus dem Prozesses in (kJ/kg)

§ ………….. zugeführte Wärme in (kJ/kg)

§ …………….Abgeführte Wärme in (kJ/kg)

Für die Wärmezufuhr und Abfuhr kann eine mittlere Temperatur wie folge definiert werden:

…………..()

……….....()

o =

§ …………zugeführte mittlere Temperatur in (K)

§ …………abgeführte mittlere Temperatur in (K)

§ …….…..zugeführte Wärme in (kJ/kg)

§ …………abgeführte Wärme in (kJ/kg)

§ ……..….Entropieänderung bei der Zustandesänderung in (kJ/kg.K)

§ ………….spezifische Entropie in (kJ/kg.K)

§ …………..spezifische Enthalpie in (kJ/kg)

· Daraus folget:

&

d.h., dass der thermische Wirkungsgrad des Clausius-Rankine-Prozesses mit () als obere Temperatur bezeichnet.

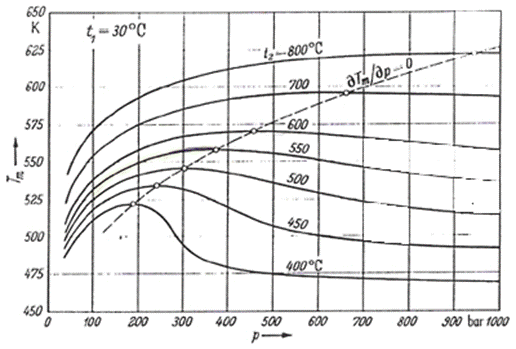
Abb.: thermodynamische Mitteltemperatur T_m der Wärmeaufnahme für T₁=303,15 K und verschiedene Frischdampftemperaturen t₂ als Funktion des Kesseldruck p [1]

mit :

o t_o = 25 ^oC

§ t_o ………………Umgebungstemperatur in (^oC)

§ t₁ ………..…….Speisewassertemperatur in (^oC)

§ t₂ ………………Frischdampftemperatur in (^oC)

§ P………………Frischdampfsdruck in (bar)

· Für die Anwendung und Berechnung des Prozesses sind neben dem Wirkungsgrad folgende anderen Zustandesgrößen notwendig:

- die Sättigungstemperaturen

- die Drücke

- die Enthalpien und Entropien

die vorgenannte Zustandesgrößen können entweder aus einen h,s-Diagramm oder Dampftafeln entnommen werden.

3. Maßnahmen zur Verbesserung des thermischen Wirkungsgrades beim Clausius-Rankine-Prozess

Wesentlichen Einfluss auf den thermischen Wirkungsgrad des Clausius-Rankine-Prozesses haben die Temperatur und der Druck des Frischdampfs, d.h. bei der Erhöhung von Druck und Temperatur des Arbeitsmittels vor der Turbine verbessert sich da folge die Wirkungsgrad des Prozesses.

Daraus bestehen Maßnahmen in der Erhöhung bzw. Absenkung der mittleren Temperatur der Wärme zu- bzw. Abfuhr. Dafür bestehen folgenden Möglichkeiten:

- Zwischenüberhitzung,

- regenerative Speisewasservorwärmung.

3.1. Die Zwischenüberhitzung

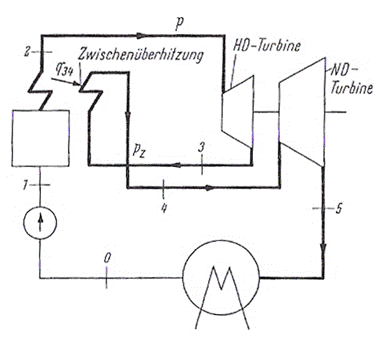
Abb.: Schaltbid einer Dampfkraftanlage mit Zwischenüberhitzung [1]

Die Zwischenüberhitzung ist ein an den Hochdruckprozess angeschlossener Teilprozess.

Dabei wird das Arbeitsmittel nach einer Teilentspannung in der Hochdruckturbine zum Dampferzeuger zurückgeführt und im Zwischenüberhitzungsteilprozess (ZÜ) wieder auf etwa die gleiche Temperatur der Hochdruckdampf erhitzt.

Die Wärmezufuhr im Zwischenüberhitzer erfolgt Isobar (3 à 4) und die Entspannung in der Niederdruckturbine (NDT) erfolgt Isentrop (4 à 5) bis auf dem Kondensatordruck.

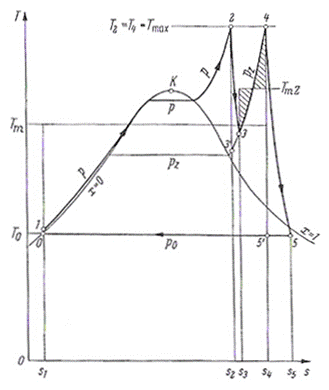
Abb.: Zustandsänderungen des Wasserdampfes beim Prozeß mit Zwischenüberhitzung [1]

Mit :

§ T_m ………die thermodynamische Mitteltemperatur der

gesamten Wärmeaufnahme

§ T_mZ……...die thermodynamische Mitteltemperatur der

Wärmeaufnahme im Zwischenüberhitzer

Der thermische Wirkungsgrad des gesamten Prozesses ergibt sich bei Vernachlässigung der Speisepumpenarbeit (s_o = s₁), wie folge:

§ ………...thermische Wirkungsgrad des gesamten Prozesses

§ …………Die Temperatur des Arbeitsmittels in (K)

§ ………….spezifische Entropie des Arbeitsmittels in (kJ/ kg.K)

§ ……...…..spezifische Enthalpie des Arbeitsmittels in (kJ/ kg)

Damit eine Verbesserung des Wirkungsgrades erreicht wird, muss die mittlere Temperatur der Wärmezufuhr für den Überhitzerteilprozess über der entsprechenden mittleren Temperatur des Hochdruckprozesses liegen.

Für die mittleren Temperatur des Hochdruckprozesses gilt:

und für die mittlere Temperatur des Teilprozesses (Zwischenüberhitzungsteil) gilt:

und für das gesamte Prozess gilt:

§ ………..mittlere Temperatur des gesamten Prozesses in (K)

§ ……..mittlere Temperatur des Hochdruckprozesses in (K)

§ ……..mittlere Temperatur des Teilprozesses (Zwischenüberhitzung) in (K)

§ …………spezifische Entropie des Arbeitsmittels in (kJ/ kg.K)

§ …………spezifische Enthalpie des Arbeitsmittels in (kJ/ kg)

Meist wird die Temperatur der Zwischenüberhitzug gleich der Temperatur der Frischdampf gewählt, so gilt:

(T₄ = T₂ = T_max)

unter diese Voraussetzug gilt:

wenn,

· Vorteile der Zwischenüberhitzung:

Aus der Verringerung der Dampfnässe in den letzten Schaufelreihen der Turbine, ergibt sich:

(1 Verminderung der Gefahr von Erosionen durch die im Dampf enthaltende Wassertropfen,

(2 Verbesserung den inneren Turbinen Wirkungsgrad.

3.2. die regenerative Speisewasservorwärmung

Die regenerative Speisewasservorwärmung nährt den Clausius-Rankine-Prozess dem idealen Carnot-Prozess an.

Bei der Speisewasservorwärmung wird das Speisewasser durch prozessinternen Wärmetauscher auf eine Temperatur aufgeheizt wird, die über die im Kondensator niedergeschlagenen Dampfstemperatur liegt.

Dies kann durch regenerativen Wärmeaustausch zwischen dem Speisewasser und Anzapfdampf aus der Turbine geschehen.

Dabei werden aus der Turbine an verschiedenen Stellen jeweils geringe Dampfstrom entnehmen. In dem Vorwärmer wird die Kondensationswärme dieser aus der Turbine anzapfendem Dampfstrom genutzt, um das Speisewasser aufzuhetzen.

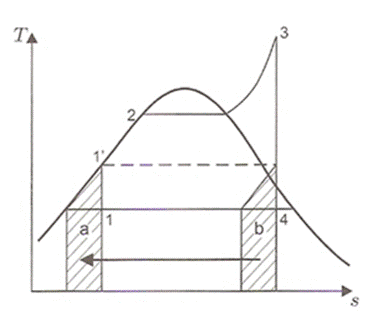
Abb.: vereinfachte Darstellung der regenerativen Speisewasservorwärmung.

Die Wärmeverschiebung von a nach b erfolgt mit Vorwärmern. Damit in diesen Apparaten eine Dampfbildung vermieden wird, bringt man das Speisewasser auf einen ausreichend hohen Druck. Dazu wird die Vorwärmstrecke in eine Nieder- und eine Hochdruckvorwärmung unterteilt [3]

Durch diese Wärmeverschiebung (b à a) wird der Prozess formal einem Carnot-Prozess angeglichen. Man spricht deshalb von einer Carnotisierung des Dampfkraftprozesses.

Andere Vorteile der Speisewasservorwärmung ist der Verringerung der an der Umgebung aus dem Kondensator abgegebene Wärmeverluste. Grund dafür ist die Verringerung der im Kondensator strömenden Abdampfmenge mit gleichbleibender Leistung der Turbine.

Für das thermische Wirkungsgrad eines Prozesses mit regenerative Speisewasservorwärmung, gilt:

§ ……..thermische Wirkungsgrad des Prozesses

§ ……..zugeführte Wärme in (kJ/ kg)

§ ……..abgeführte Wärme in (kJ/ kg)

§ ……….Temperatur des Arbeitsmittels in (K)

§ ……….Entropie des Arbeitsmittels in (kJ/ kg.K)

§ ……….Enthalpie des Arbeitsmittels in (kJ/ kg)

§ …...….Enthalpie des Arbeitsmittels in siedendem

Flüssigkeitszustand in (kJ/ kg)

4. Beispiele für Stationen mit Dampfkraftprozess

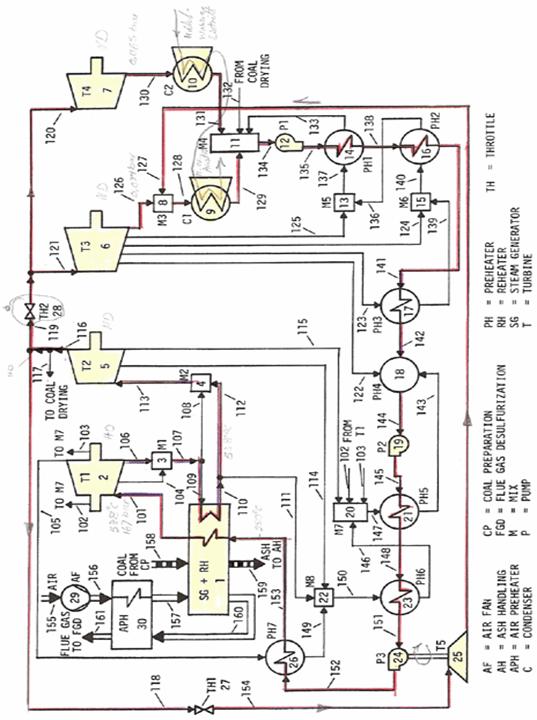
4.1. Grundfließbild der Harry Allen Station (Nevada- USA) [2]

5. fragen

1- Erläutern Sie die Komponenten des Clausius-Rankine-Prozesses (CRP).

2- Zeichen Sie Varianten des CRP in T,s-Diagramm und die dazugehörigen Schaltschemen

3- Durch welche Maßnahmen kann der CRP verbessert werden? Erläutern Sie mögliche Maßnahmen.

6. Literatur

[1] Baehr, H.D.; Thermodynamik, Springer-Verlag, 12.Auflage, Berlin, 2005

[2] Tsatsaronis, G., Umdruck zur Vorlesung Energietechnik an der TU- Berlin, 2006

[3] Strauß, K.; Kraftwerkstechnik, Springer-Verlag, 5.Auflage, Berlin, 2006

[4] Karl, J.; Dezentrale Energiesysteme, Oldenbourg- Verlag, München, 2004

[5] VDI Wärmeatlas; VDI-Verlag, 8.Erweiterte Auflage, Düsseldorf, 1996